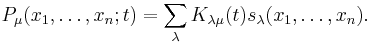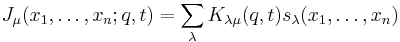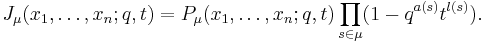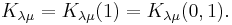Kostka polynomial

In mathematics, a Kostka polynomial or Kostka–Foulkes polynomial K_λμ(q, t), named after Carl Kostka, is a polynomial in two variables with non-negative integer coefficients depending on two partitions λ and μ. Sometimes the variable q is fixed to be 0 in which case the polynomials are denoted by K_λμ(t) = K_λμ(0,t). The two-variable polynomials are also called Macdonald–Kostka polynomials or q,t-Kostka polynomials. There are two slightly different versions of them, one called transformed Kostka polynomials.

The one variable polynomials can be used to express Hall-Littlewood polynomials P_μ as a linear combination of Schur polynomials s_λ:

$P_\mu(x_1,\ldots,x_n;t) =\sum_\lambda K_{\lambda\mu}(t)s_\lambda(x_1,\ldots,x_n).\$

The Macdonald–Kostka polynomials can be used to express Macdonald polynomials (also denoted by) P_μ as a linear combination of Schur polynomials s_λ:

$J_\mu(x_1,\ldots,x_n;q,t) =\sum_\lambda K_{\lambda\mu}(q,t)s_\lambda(x_1,\ldots,x_n)\$

where

$J_\mu(x_1,\ldots,x_n;q,t) = P_\mu(x_1,\ldots,x_n;q,t)\prod_{s\in\mu}(1-q^{a(s)}t^{l(s)}).\$

Kostka numbers are special values of the 1 or 2 variable Kostka polynomials:

$K_{\lambda\mu}= K_{\lambda\mu}(1)=K_{\lambda\mu}(0,1).\$

Examples

References

Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144, http://www.oup.com/uk/catalogue/?ci=9780198504504
Nelsen, Kendra; Ram, Arun (2003), "Kostka-Foulkes polynomials and Macdonald spherical functions", Surveys in combinatorics, 2003 (Bangor), London Math. Soc. Lecture Note Ser., 307, Cambridge: Cambridge Univ. Press, pp. 325–370,, arXiv:math/0401298, MR 2011741
Stembridge, J. R. (2005), Kostka-Foulkes Polynomials of General Type, lecture notes from AIM workshop on Generalized Kostka polynomials, http://www.aimath.org/WWN/kostka

Kostka polynomial

Examples

References

External links